Plausible values are imputed values that resemble individual test scores and have approximately the same distribution as the latent trait being measured. Plausible values were developed as a computational approximation to obtain consistent estimates of population characteristics in assessment situations where individuals are administered too few items to allow precise estimates of their ability. Plausible values represent random draws from an empirically derived distribution of proficiency values that are conditional on the observed values of the assessment items and the background variables. The random draws from the distribution represent values from the distribution of scale scores for all adults in the population with similar characteristics and identical response patterns. These random draws or imputations are representative of the score distribution in the population of people who share the background characteristics of the individual with whom the plausible value is associated in the data.
Let
y represent the responses of all
sample examinees to background and attitude questions, along with design variables such as school membership, and let
q represent the subscale proficiency values. If
q were known for all sampled examinees, it would be possible to compute a statistic
t(
q,
y) - such as a subscale or
subpopulation sample mean,
sample percentile point, or
sample regression coefficient - to estimate a corresponding
population quantity
T. A function U(
q,
y) -e.g., a
jackknife estimate - would be used to gauge sampling uncertainty, as the variance of
t around
T in repeated samples from the
population.
Because the 3PL model is a latent variable model, however, q values are not observed even for sampled students. To overcome this problem, we consider q as "missing data" (Rubin, 1987) and approximate t(q,y) by its expectation given (x,y), the data that actually were observed, as follows:
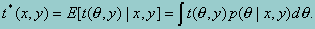
It is possible to approximate t* using random draws from the conditional distributions, p(q|xi,yi) of the subscale proficiencies given the item responses x1 and background variables yi for sampled adult i. These values are referred to as "imputations" in the sampling literature and "plausible values" here. The value of q for any respondent that would enter into the computation of t is thus replaced by a randomly selected value from the conditional distribution p(q|xi,yi). Rubin (1987) suggests repeating this process several times so that the uncertainty associated with the fact that q's are not observed can be quantified. The variance among them reflects uncertainty due to not observing q and must be added to an estimate of U(q,y).
It cannot be emphasized too strongly that plausible values are not test scores for individuals in the usual sense. Plausible values are offered only as intermediary computations for calculating integrals in order to estimate population characteristics. When the underlying model is correctly specified, plausible values will provide consistent estimates of population characteristics, even though they are not generally unbiased estimates of the proficiencies of the individuals with whom they are associated. The key idea lies in a contrast between plausible values and the more familiar q estimates of educational measurement that are in some sense optimal for each examinee. Point estimates that are optimal for individual examinees have distributions that can produce inconsistent estimates of population characteristics. Plausible values, on the other hand, are constructed explicitly to provide consistent estimates of population effects.
Mislevy, R. J. (1991). Randomization-based inferences about latent variables from complex samples. Psychometrika, 56(2), 177-196.
Mislevy, R. J., Johnson, E. G., & Muraki, E. (1992). Scaling procedures in NAEP. Journal of Educational Statistics, 17(2), 131-154.
Rubin, D. B. (1987). Multiple Imputation for Non-response in Surveys. New York: Wiley.
This is the overview of the MML Regression.
Because in NAEP each respondent is administered relatively few items in a scaling area, the uncertainty associated with his or her q, or ability, is too large to be ignored and thus estimates of q can be seriously biased. To address this problem, NAEP computes five plausible values on each subscale for each student. These plausible values are constructed from the results of a comprehensive marginal maximum likelihood regression equation including all of NAEP’s background data plus an appropriate random component. By using these plausible values, secondary analysts can obtain consistent estimates of population characteristics even though individual point estimates for each individual might be biased.