Marginal Maximum Likelihood

Table Of Contents

Manual
- Getting Started
  - Starting the Program
  - Retrieving Data
  - Manipulating Data
  - Saving and Re-running Actions
    - Reviewing and accessing the code
    - Saving and re-running statistical models
- Sampling
- Procedures
  - Measurement Models
  - MML Models for Test Data
  - Other Available Procedures
- Graphics
- Tools
  - Estimation Methods
  - Optimization Techniques
  - Variance Estimation
- Post-hoc Procedures
- More user input instructions
  - The User Interface
    - Completed Run Queue
    - The Variable List
  - Input Instructions
  - Options
  - Output Precision
- Glossary of Terms and Symbols

Marginal Maximum Likelihood (MML) estimation extends the ideas of Maximum Likelihood (ML) estimation by applying them to situations when the variables of interest are only partially observed. MML estimation provides estimates of marginal (i.e., aggregate) parameters that are the most likely to have generated the observed sample data. MML estimation proves useful when one is interested in estimating the mean and variance of a scale from survey data that provides only imperfect measurement of the target construct.

In marginal maximum likelihood (MML) estimation, the likelihood function incorporates two components: a) the probability that a student with a specific "true score" will be sampled from the population; and b) the probability that a student with that proficiency level produces the observed item responses. Multiplying these probabilities together for all possible proficiency levels is the basis of the likelihood function for the marginal maximum likelihood estimate. More formally, by defining q to represent a proficiency level, and z_i to denote student i's responses to test items, then the value of the likelihood function for individual i is:

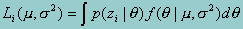
The integral appearing in this equation is really just a way of averaging the probability of observing the survey response (z_i) given a value of q (that is, a level of the underlying construct) over the distribution of q (that is, over all possible values of q, weighted by the probability of sampling each possible value of q). The overall likelihood function is the product of all of the individual likelihood functions for individuals in the sample.

One generally works with the logarithm of the likelihood function (rather than the function itself) for two reasons: 1) the log-likelihood reaches a maximum at the same parameter estimates as the likelihood function reaches its maximum (that is, an change in the likelihood always corresponds to a change in the same direction of the log-likelihood); and 2) logs can be summed over the observations, and sums are easier to work with than products. The best estimates of m and s² are those that yield the highest value of (i.e., the maximum) of the likelihood (and log-likelihood) function.

Note that the model never requires a point estimate of proficiency (q) for each individual. Rather the method "tries" all possible values, weighting each one by the probability that a random draw from a population with mean m and variance s² would yield it. In this way, the method estimates the distribution of proficiency in the population without ever estimating proficiency for each individual. This is why the method is called "marginal"-because it yields point estimates of the group or subgroup parameters without requiring point estimates for individual students.

The integral in the above likelihood equation is difficult to evaluate, so instead, it is approximated by summation over a finite number of points (the "quadrature points"). To do so, we identify a range within which all observations are virtually certain to fall and select equally spaced points along this interval. For example, if q is a standard normal (0,1) variate, it makes sense to have the quadrature points range between about -4 and 4 (99.994% of cases will fall in this range). Thus, letting q={1,2,...Q} for Q quadrature points (q_q), one can re-write the individual likelihood function as:

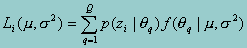
Now, we note that p(z_i|q_q) can be directly calculated. The probability of z_i|q is the probability of observing the responses to the test items z given an ability level of q_q. This can be calculated directly from the IRT model and the estimated item parameters. Thus, the sample likelihood is calculated by summation of the product of two densities across quadrature points for each individual, taking logs, then summing the log-likelihoods across individuals.

The second term in the equation is the probability of observing a value of q given its distribution in the population (generally assumed normal with a mean m and a standard deviation of s).

The goal then is to find the values of the two-parameters (m,s) that maximize the likelihood function. This is typically done by some iterative method that tries some values of the parameters, evaluates the function, then adjusts the provisional parameter estimates to increase the function.

Andersen, E. B., & Madsen, M. (1977). Estimating the parameters of a latent population distribution. Psychometrika, 42, 357-374.

Bock, R. D., & Aitkin, M. (1982). Marginal Maximum Likelihood estimation of item parameters: application of an EM algorithm. Psychometrika, 46, 443-459.

Mislevy, R. J. (1985). Estimation of latent group effects. Journal of the American Statistical Association, 80, 993-997.

Mislevy, R. J. (1991). Randomization-based inference about latent variables from complex samples. Psychometrika, 56, 177-196.

Marginal (MML) models were introduced in NAEP in 1984 to estimate subgroup parameters in light of the missing data created by the use of BIB spiraling item sampling procedures. Under BIB spiraling, no one student is administered enough items to allow precise estimation of his or her ability through maximum likelihood (ML) estimation. MML models permit the estimation of group or subgroup parameters (e.g., mean, variance) without requiring point estimates of proficiency for individual students. NAEP uses the plausible values methodology to provide secondary analysts with a way to analyze NAEP data and estimate the population characteristics obtained in the marginal analyses.