In a situation where the first derivative of the log likelihood function is available, an efficient method of finding the maximum of the pseudo log-likelihood equation is one developed by Bernt, Hall, Hall and Hausman [BHHH] (1974) based on the Newton-Raphson algorithm. This method is based on starting from some easy but imprecise estimate of the Maximum Likelihood estimators, then taking a succession of 'steps' based on the value of the first derivatives until a solution is found.
The Newton-Raphson
algorithm, also known as Newton's method, is an iterative process for finding relative extremes of non-linear functions. Using the Newton-Raphson
algorithm requires one to have both the analytic first and second derivatives of the log-likelihood function with respect to 2. Given a set of start values,
q0, we move one step closer towards the
maximum likelihood (ML) solution by adding the product of the first and second derivatives of log likelihood function,
l, to the current point:

Where S(q) is the vector of first derivatives with respect to the parameters, known as the score vector, and H(q) is the matrix of second derivatives, known as the Hessian matrix. While Newton's method has many desirable properties in a range of maximum likelihood problems, it only works when the matrix of second derivatives is positive definite. Unfortunately, this is not always the case, especially in early iterations. The BHHH method substitutes the sum of each term of the score vector multiplied by itself, i.e.,
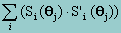
for the negative Hessian matrix, thus eliminating the need for second derivatives and guaranteeing a positive definite matrix everywhere. The above process is repeated in successive steps until one of three quantities is sufficiently small: 1) The difference between the parameter estimates, i.e., | qj - qj+1| ,2) the difference between the likelihood estimates, i.e., lj+1 - lj, and 3) the score vector S(qj+1). How small is sufficiently small depends on the behavior of the model, but is typically 0.01 or less. Thus, the only values needed for optimization are 1) the likelihood function (to check for convergence), and 2) the first derivatives. The BHHH method has proven to work well even when start values are less than optimal.
Berndt, E. K., Hall, B. H., Hall, R. E., & Hausman, J. A. (1974). Estimation and inference in nonlinear structural models. Annals of Economic and Social Measurement, 3/4, 653-665.