The EM algorithm is one of several optimization techniques that can be used to obtain Marginal Maximum Likelihood (MML) estimates of item parameters based on IRT models when the variable of interest (e.g., ability) is only partly observed. This algorithm consists of iterating two-phase 'steps' until the maximum likelihood estimator is found. Phase one of each iteration, known as the E-step (where E stands for expectation), is based on computing the provisional expected frequency and the provisional expected sample size. Phase two, known as the M-step (where M stands for maximization), is based on computing MML estimates of the parameter by maximizing the log-likelihood function. Each estimation process is repeated until the values become stable at a given level of precision specified by the analyst.
The EM algorithm was developed as a generalization of several different methods for estimating a parameter that is only partly observed (Dempster, Laird, and Rubin, 1977). This algorithm has become widely used because of its conceptual simplicity and ease of implementation. However, this algorithm has the disadvantages of converging slowly and generally only linearly.
The EM algorithm is an iterative one, with each iteration consisting of two steps. The first step (know as the E step), computes the expected log-likelihood function of the complete data, lj, based on the observed data, Dp, and the best current estimate of the parameter of interest, qj. The second step (know as the M step), consists of re-estimating the parameter of interest q based on maximizing the newly estimated log-likelihood function lj. The algorithm is thus:
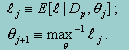
This two-step process is repeated until convergence, specified as a given precision criterion.
Bock, R. D., & Aitkin, M. (1982). Marginal Maximum Likelihood estimation of item parameters: application of an EM algorithm. Psychometrika, 46, 443-459.
Dempster, A. P., Laird, N. M., & Rubin, D. B. (1977). Maximum likelihood from incomplete data via the EM algorithm (with Discussion). Journal of the Royal Statistical Society, 1977 Series B, 39, 1-38.
Muraki, E. (1992). A generalized partial credit model: Application of an EM algorithm. Applied Psychological Measurement, 16, 159-176.