NAEP Tables

Table Of Contents

Manual
- Getting Started
  - Starting the Program
  - Retrieving Data
  - Manipulating Data
  - Saving and Re-running Actions
    - Reviewing and accessing the code
    - Saving and re-running statistical models
- Sampling
- Procedures
  - Measurement Models
  - MML Models for Test Data
  - Other Available Procedures
- Graphics
- Tools
  - Estimation Methods
  - Optimization Techniques
  - Variance Estimation
- Post-hoc Procedures
- More user input instructions
  - The User Interface
    - Completed Run Queue
    - The Variable List
  - Input Instructions
  - Options
  - Output Precision
- Glossary of Terms and Symbols

NAEP Tables

The NAEP tables analysis is a special format for analyzing NAEP data. It builds upon the MML composite regression model to calculate the specific estimates that current NAEP plausible values are designed to approximate. Currently, NAEP tables present the percent of students above specified
cutscores (e.g., NAEP achievement levels) for composite scales. These estimates are based on the multivariate posterior distributions from which plausible values are drawn.

Corresponding to each examinee i, the percent above a cutscore c is:

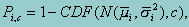
and the population cut point percent is then

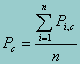
The variance of the above percent estimation can be decomposed into two parts. The first part is due to the uncertainty of the parameter estimation. For each examinee, this part of variance is:

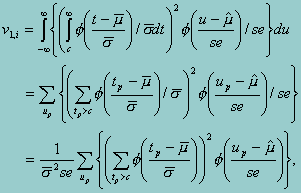
where t_p, u_p are two sets of quadrature points, and se is the standard error of the prior estimate û = 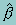. Thus, the first part of the population variance is the sample mean of the above individual variances. The second part is the sample variance among the estimated individual percent above the cutscore p_i,c. In other words, the variance (or standard error) of the estimated cut point percent is: mean(v_1,i) + var(p_i,c)..

Cohen, J., & Jiang, T. (1998). Composite Assessment Scales and NAEP Analyses. Washington, DC: American Institutes for Research.

To run NAEP Tables left-click on the Statistics Menu and select "NAEP Table." The following dialogue box will open:

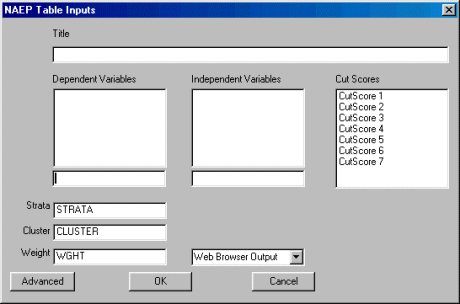
Specify the independent variable and the dependent variable. There are several specific requirements for variables when running the NAEP Table. The user may specify only a single, categorical independent variable. A future release will allow the selection of multiple.

This procedure reproduces estimates of percent of students above specified cut scores (e.g. NAEP achievement levels) as presented in NAEP reports.