Bayesian estimation provides an alternative to the classical or sampling theory approach. In contrast to classical statistical inference where population parameters are treated as fixed, Bayesian inference involves assigning probabilities to the possible values of a population parameter, and through Bayes' theorem modifying these probabilities based on the evidence contained in the
In classical statistical inference, the parameters of the population are considered to be fixed, and the particular distribution that results from a given sample is taken as a variable. Bayesian inference, by contrast, treats the data that one has observed as given and treats the actual parameters as likely as any other. One then modifies this distribution with the likelihood function drawn from the data to create a new distribution, known as the posterior distribution, from which one can draw posterior probabilities for
the values of the
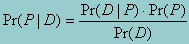
In a situation where we want to know the probabilities of each of several P's that are, taken together, exclusive and exhaustive, the probability of D can be written as a weighted sum of the conditional probabilities of D given each Pi where the weights are the probabilities for each Pi. Thus for the event Pi in a situation where there are k different P's, the above equation becomes
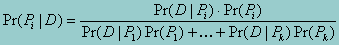
which is Bayes' theorem for the discrete case with k different P's.
In the original applications of Bayes' theorem, the P's represented different populations; however, they can also represent different possible values for a given parameters of a single population. In either case, D represents the data being used in the estimation of the model.
If the possible values of some characteristic of a population are represented by a continuous variable rather than a set of k discrete possible values, the probability that the parameters has a particular discrete value becomes zero. Thus, each Pi becomes a range, and Pr Pi becomes the probability that the va e difficulty one sometimes encounters when trying to fit one's assumptions or prior knowledge into a distribution. It is difficult, at times, to form a likelihood function based on prior information, and the information can be easily misrepresented. In addition, the posterior distribution usually has a very complex form.
Bayes, T. (1763). Essay towards solving a problem in the doctrine of chances. Philosophical Transactions. Royal Society, London 53, 370-418. (Reprinted in Biometrika, 1958, 45, 293-315).
Box, G. E. P., & Tiao, G. C. (1973). Bayesian Inference in Statistical Analysis. Reading, MA: Addison-Wesley.
Iversen, G. R. (1984) Bayesian statistical inference. Sage University Paper 96: Quantitative Applications in the Social Sciences.