Conditional Independence

Table Of Contents

Manual
- Getting Started
  - Starting the Program
  - Retrieving Data
  - Manipulating Data
  - Saving and Re-running Actions
    - Reviewing and accessing the code
    - Saving and re-running statistical models
- Sampling
- Procedures
  - Measurement Models
  - MML Models for Test Data
  - Other Available Procedures
- Graphics
- Tools
  - Estimation Methods
  - Optimization Techniques
  - Variance Estimation
- Post-hoc Procedures
- More user input instructions
  - The User Interface
    - Completed Run Queue
    - The Variable List
  - Input Instructions
  - Options
  - Output Precision
- Glossary of Terms and Symbols

Conditional independence is an assumption that the probability of correct responses is independent across items given the respondent’s ability. This assumption implies that (1) the probability of correctly answering assessment items is unrelated to the respondent’s background characteristics, and (2) item response probabilities depend only on the examinee’s ability, not on the position of the items in the assessment.

Item response theory models are based on the assumption of conditional independence. This implies that the probability of correct responses by an individual to a set of items is independent across items, given the individual’s proficiency. Conditional on the examinee’s latent ability (e.g. verbal ability, mathematical reasoning ability), q_k, the joint probability of a particular response pattern x = (x₁,...,x_n) on a subscale is simply the product of the examinee’s response probabilities to individual items:

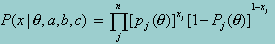
Conditional independence implies that examinees’ response probabilities are unrelated to background variables (y), given their proficiency. An examinee’s latent trait or ability contains all the systematic information about an examinee’s proficiency on a test. This means that answers to individual items will be randomly related to or independent of background variables, once ability has been partialled out:

P(x|q, a,b,c,y)=P(x|q, a,b,c)

A second implication of conditional independence is that the item response probabilities depend only on the examinee’s ability and the specified item parameters, and not on the position of the item in the booklet, the content of the items around an item of interest, or the test administration conditions. This however is not true in every case, and violation of this assumption can occur. To detect violations of conditional independence, differential item functioning analyses (DIF) and item fit statistics are used to check for bias across subgroups and time periods.

Lord, F. M., & Novick, M. R. (1968). Statistical Theories of Mental Test Scores. Reading, Mass: Addison-Wesley.

Hambleton, R. K., & Swaminathan, H. (1985). Item Response Theory: Principles and Applications. Boston: Kluwer-Nijhoff Publishing.

Currently, checks against the violation of the assumption of conditional independence must be performed through some other statistical software package.

The item response theory (IRT) models used to estimate examinees’ proficiency on the NAEP assume conditional independence. To detect violations of this assumption, checks on the plausibility of this assumption include the following:

Item operating characteristics among distinct gender and ethnicity groups are compared (i.e., differential item functioning analyses (DIF) analyses).
When a subscale extends over age groups, evidence is sought of different operating characteristics over ages.
When a scale extends over time, evidence is similarly sought as to whether an item’s relative operating characteristics have changed over time, over and above differences that can be accounted for by changes in the overall distribution.