The term "plausible values" refers to imputations of test scores based on responses to a limited number of assessment items and a set of background variables. Rather than require users to directly estimate marginal maximum likelihood procedures (procedures that are easily accessible through AM), testing programs sometimes treat the test score for every observation as "missing," and impute a set of pseudo-scores for each observation. The imputations are random draws from the posterior distribution, where the prior distribution is the predicted distribution from a marginal maximum likelihood regression, and the data likelihood is given by likelihood of item responses, given the IRT models.
This section will tell you about analyzing existing plausible values. To learn more about where plausible values come from, what they are, and how to make them, click here.
If you are interested in the details of a specific statistical model, rather than how plausible values are used to estimate them, you can see the procedure directly:
When analyzing plausible values, analyses must account for two sources of error:
- Sampling error; and
- Imputation error.
This is done by adding the estimated sampling variance to an estimate of the variance across imputations.
The particular estimates obtained using plausible values depends on the imputation model on which the plausible values are based.
To estimate a target statistic using plausible values,
- Estimate the statistic once for each of m plausible values. Let these estimates be
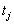, where j={1,2,...m} for the m plausible values.
- Calculate the average of the m estimates to obtain your final estimate:
.
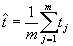If your are interested in the details of the specific statistics that may be estimated via plausible values, you can see:
To estimate the standard error, you must estimate the sampling variance and the imputation variance, and add them together:
- Estimate the standard error by averaging the sampling variance estimates across the plausible values. In practice, most analysts (and this software) estimates the sampling variance as the sampling variance of the estimate based on the estimating the sampling variance of the estimate based on the first plausible value. By default, AM estimates the sampling variance via Taylor series approximation. Let V represent this variance.
- Estimate the imputation variance as the variance across plausible values. This is given by
.
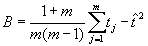- The final estimate of the standard is
.
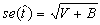Mislevy, R. J. (1991). Randomization-based inferences about latent variables from complex samples. Psychometrika, 56(2), 177-196.
Mislevy, R. J., Johnson, E. G., & Muraki, E. (1992). Scaling procedures in NAEP. Journal of Educational Statistics, 17(2), 131-154.
Rubin, D. B. (1987). Multiple Imputation for Non-response in Surveys. New York: Wiley.
Running the Plausible Values procedures is just like running the specific statistical models: rather than specify a single dependent variable, drop a full set of plausible values in the dependent variable box. For example, NAEP uses five plausible values for each subscale and composite scale, so NAEP analysts would drop five plausible values in the dependent variables box. Be sure that you only drop the plausible values from one subscale or composite scale at a time.
Other than that, you can see the individual statistical procedures for more information about inputting them:
NAEP uses five plausible values per scale, and uses a jackknife variance estimation. Currently, AM uses a Taylor series variance estimation method. This results in small differences in the variance estimates. Most of these are due to the fact that the Taylor series does not currently take into account the effects of poststratification.
NAEP's plausible values are based on a composite MML regression in which the regressors are the principle components from a principle components decomposition. Essentially, all of the background data from NAEP is factor analyzed and reduced to about 200-300 principle components, which then form the regressors for plausible values.
To learn more about the imputation of plausible values in NAEP, click here.