Two-Parameter Logistic Model

Table Of Contents

Manual
- Getting Started
  - Starting the Program
  - Retrieving Data
  - Manipulating Data
  - Saving and Re-running Actions
    - Reviewing and accessing the code
    - Saving and re-running statistical models
- Sampling
- Procedures
  - Measurement Models
  - MML Models for Test Data
  - Other Available Procedures
- Graphics
- Tools
  - Estimation Methods
  - Optimization Techniques
  - Variance Estimation
- Post-hoc Procedures
- More user input instructions
  - The User Interface
    - Completed Run Queue
    - The Variable List
  - Input Instructions
  - Options
  - Output Precision
- Glossary of Terms and Symbols

The Two-Parameter Logistic model uses an item response theory (IRT) model that specifies the probability of a correct response as a logistic distribution in which items vary in terms of their difficulty and discrimination. It is typically applied to multiple choice or short constructed-response items that are scored either correct or incorrect, and do not appear to allow for guessing.

The 2PL (Birnbaum, 1968), generalizes the one-parameter logistic, or Rasch, model by allowing items to vary not only in terms of their difficulty (b) but also in terms of their ability to discriminate (a) among individuals of various proficiency. As with the Rasch model, the 2PL assumes that the probability of a correct guess is zero. The fundamental equation of the 2PL is the probability that a person whose proficiency on scale k is characterized by the unobservable variable q_k will respond correctly to item j:

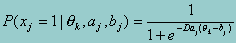
where
x_j = the response to item j, 1 if correct and 0 if not;
a_j = the slope of parameter of item j, characterizing its sensitivity to
proficiency, where a_j>0;
b_j = the threshold parameter of item j, characterizing its difficulty;
D = an arbitrary scaling constant typically set to 1.7 to approximate results
from the normal ogive model.

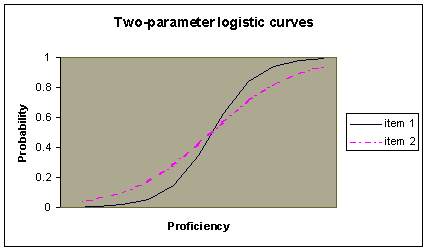
The figure below illustrates the 2PL logistic curves for two items of similar difficulty but different discrimination parameters. The addition of the a parameter allows the slopes of the curves to vary, indicating how discriminating the item is. The steeper the slope of the curve, the more discriminating the item. In this illustration, item 1 is more discriminating than item 2.

logisticcurves

Birnbaum, A. (1968). Some latent trait models and their use in inferring an examinee’s ability. In F. M. Lord & M. R. Novick, Statistical Theories of Mental Test Scores (pp. 397 - 472). Reading, MA: Addison-Wesley Publishing.

Crocker, L., & Algina, J. (1986). Introduction to Classical & Modern Test Theory. Fort Worth: Harcourt Brace Jovanovich College Publishers.

Hambleton, R. K., & Swaminathan, H. (1995). Item Response Theory: Principles and Applications. Norwell, MA: Kluwer Academic Publishers.

Currently the parameters of the Two-Parameter Logistic Model must be estimated through some other statistical software package and imported into AM. Future versions of AM software will allow the user to estimate both item and ability parameters.

NAEP currently uses the Two-Parameter Logistic model (2PL) to estimate the probability of an individual’s correct response to multiple choice or short constructed-response items scored either correct or incorrect and in a format that does not appear to allow for guessing. Since the item parameters and ability parameters are unobservable, there is a certain degree of indeterminacy in the model. This identification problem is solved in NAEP through Bayesian estimation by specifying prior belief for the parameters in the model. The prior distribution for the slope parameter, a, is specified as log normal with mean = 0 and standard deviation = 0.5. The prior for the threshold parameter, b, is specified as normal with mean = 0 and standard deviation = 2.