Taylor Series Expansion

Table Of Contents

Manual
- Getting Started
  - Starting the Program
  - Retrieving Data
  - Manipulating Data
  - Saving and Re-running Actions
    - Reviewing and accessing the code
    - Saving and re-running statistical models
- Sampling
- Procedures
  - Measurement Models
  - MML Models for Test Data
  - Other Available Procedures
- Graphics
- Tools
  - Estimation Methods
  - Optimization Techniques
  - Variance Estimation
- Post-hoc Procedures
- More user input instructions
  - The User Interface
    - Completed Run Queue
    - The Variable List
  - Input Instructions
  - Options
  - Output Precision
- Glossary of Terms and Symbols

Taylor Series Expansion - DRAFT VERSION

Taylor series expansion is a method for obtaining robust variance estimators for complex survey data with stratified, cluster sampling with unequal probabilities of selection. The Taylor series is used to obtain an approximation to some nonlinear function, and then the variance of the function is based on the Taylor series approximation to the function. This general computational procedure can be applied to a variety of nonlinear estimators such as regression coefficients. In complex survey, this method of approximation is applied to the PSU totals within the stratum.

The roots of the score functions constitute sets of estimating functions (Godambe, 1960). Godambe (1960) proves an optimal property of maximum likelihood estimating functions in simple random samples, and Godambe and Thompson (1986) show that the standard p - weighted estimating function retain this optimal property in unequal probability samples. Thus, the log-likelihood function and its derivatives at each observation can be multiplied by the inverse probability of inclusion in the sample, yielding optimal estimating functions.

Binder (1983) has extended the utility of this result by providing a general approach to approximating the variances of the estimates from general estimating functions. He has shown that under very general conditions, the Taylor series approximation of the sampling variance of estimates can be applied to any arbitrary estimating function, and is approximately

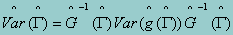
This is popularly known as Binder's sandwich estimator. In this case, the outer terms are approximated by 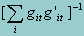evaluated at the converged parameter values. The variance term in the center is the estimated variance/covariance matrix of the first derivatives. Note that this is simply the variance/covariance matrix of a set of population totals (the summed first derivatives). In a stratified, clustered, unequally weighted sample, one can estimate this as the B estimator of the stratified, between-PSU variance.

Binder, D. A. (1983). On the variances of asymptotically normal estimators from complex surveys. International Statistical Review, 51, 279-292.

Cohen, J., & Jiang, T. (in press). Comparison of partially measured latent traits across nominal subgroups. Journal of the American Statistical Association, 94.

Godambe, V. P. (1960). An optimum property of regular maximum likelihood estimation. Annals of Mathematical Statistics, 31, 1208-1212.

Godambe, V. P., & Thompson, M. E. (1986). Parameters of superpopulation and survey population: Their relationships and estimation. International Statistical Review, 54, 127-138.

NAEP uses the jackknife repeated replication (JRR) method to obtain robust variance estimators of statistics presented in NAEP reports. While the JRR method provides a good approximation of the true sampling variability, as the number of pseudo-replicated samples increases, its computational requirements become intractable. The Taylor series expansion method offers an alternative method to variance estimation that is computationally more efficient than the JRR method.