A total is the sum of the values of a variable across observations, often weighted (by
sample weights
to estimate the sum of values across the whole population. Sometimes totals hold inherent interest themselves, as when
a policy-maker may try to estimate the number of girls in schools in a state or nation. More often, totals are estimates
in support of other statistics.
Many statistics can be viewed as a function of sample totals. For example, the mean is the ratio of the sum of
a variable's values, divided by the sum of sample inclusion indicators (or the weighted values divided by the
sum of weights). Many statistical procedures use population totals in estimation, including,
The totals procedure estimates the population total from the sample data as
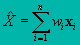
where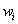 
is a sample weight, usually representing the inverse of the probability of selection, sometimes adjusted for nonresponse and poststratified to match population totals of some other variables.
The variance matrix for the population totals is given by,
.
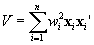Standard errors can be estimated by Taylor-series expansion or a replication, such as the jackknife.
Lee, E. S., Forthofer, R. N., & Lorimor, R. J. (1989). Analyzing Complex Survey Data. Sage University Papers 71: Quantitative Applications in the Social Sciences.
Särndal, C. E., Swensson, B., & Wretman, J. (1992). Model Assisted Survey Sampling. New York: Springer-Verlag.
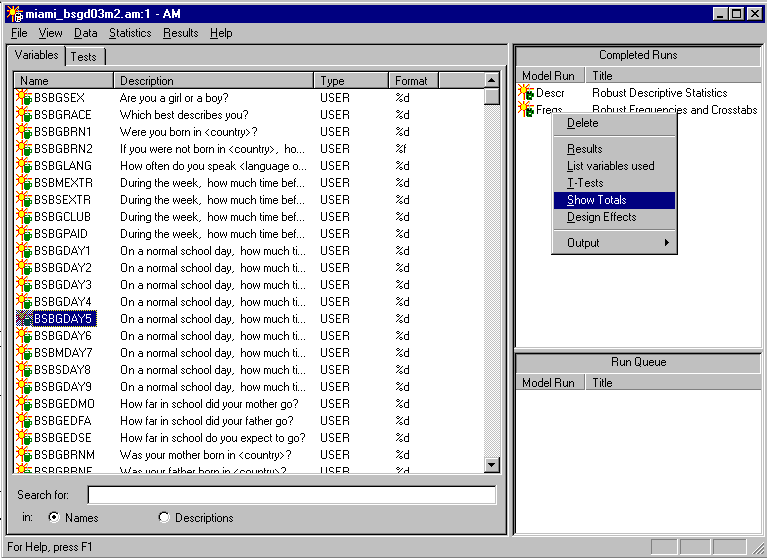
AMpresents estimates of population totals when sample weights are designed to sum to the sample total.
Most procedures print a "Weighted N" indicating the estimated population size (the sum of weights). For the descriptive
procedure, simply multiply the total weight by the mean to get the estimated population sum.
Estimated population totals tend to be more useful for categorical data. AM will generate produce totals
as a post-hoc procedure from the Frequencies procedure. After running a Frequencies procedure,
right click on the icon in the Completed Run Queue and select the "Show Totals." It looks like this:
