The generalized partial credit model (GPCM) is an item response theory (IRT) model developed for situations where item responses are contained in two or more ordered categories. Items are conceptualized as a series of ordered steps where examinees receive partial credit for successfully completing a step. Steps correspond to the various levels of performance needed to complete an item. The GPCM is formulated based on the assumption that each probability of choosing the k-th category over the k - 1-th category is governed by the dichotomous response model.
The generalized partial credit model (GPCM) is an IRT model developed to analyze partial credit data, where responses are scored 0,1,…, k, where k is the highest score category for the item.
Masters (1982) developed the partial credit model (PCM) by formulating a polytomous rating response model based on the Rasch (1960) dichotomous model. In Masters’ formulation, the probability of choosing the kth category over the k - 1th category of item i is governed by the dichotomous response model. Let Pjk(q) denote the specific probability of selecting the kth category from mj possible categories of item j. For each adjacent categories, the probability of the specific categorical response k over k - 1 is given by the conditional probability:
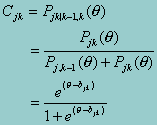
where k = 1,2,..., mj
Note that in this model, all items are assumed to have uniform discriminating power.
Muraki (1992) extented Masters’ PCM by relaxing the assumption of uniform discriminating power of test items based on the two-parameter (2PL) logistic response model. In Muraki’s formulation, the probability of choosing category k over category k - 1 is given by the conditional probability:
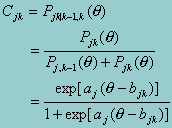
where k = 1,2,...,mj. The above equation can be written as
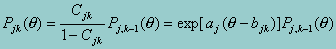
After normalizing each Pjk(q) so that S Pjk(q) = 1, the GPCM is written as
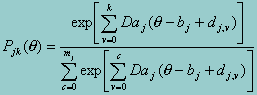
where D, is a scaling constant set to 1.7 to approximate the normal ogive model, aj is a slope parameter , bj is an item location parameter , and dj,v is a category parameter . The slope parameter indicates the degree to which categorical responses vary among items as q level changes. With mj categories, only mj - 1 category parameters can be identified.
Indeterminacies in the parameters of the GPCM are resolved by setting dj,0 = 0 and setting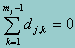 
. Muraki (1992) points out that bj - dj,k is the point on the q scale at which the plots of Pj,k-1(q) and Pjk(q) intersect and so characterizes the point on the q scale at which the response to item j has equal probability of falling in response category k -1 and falling in response category k.
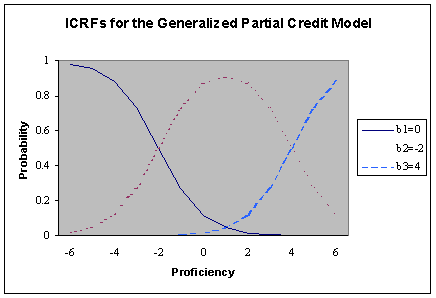
The figure below illustrates the item category response functions (what is known as item characteristic curves for dichotomous items) for a GPCM item with parameters a=1 and b=(0,-2,4). It is clear from this graph that the point of intersection of Pj,k-1(q) and Pjk(q) corresponds to an equal probability (i.e., P = .5) of being in category k -1 or category k.
Masters, G. N. (1982). A Rasch model for partial credit scoring. Pscychometrika, 47, 149-174.
Muraki, E. (1992). A generalized partial credit model: Application of an EM algorithm. Applied Psychological Measurement, 16, 159-176.
Currently the parameters of the Generalized Partial Credit Model must be estimated through some other statistical software package and imported into AM. Future versions of AM software will allow the user to estimate both item and ability parameters.
NAEP uses the generalized partial credit model to analyze polytomous item where responses are contained in two or more ordered categories. Indeterminacies in the parameters of the GPCM are resolved by setting
dj,0 = 0 and setting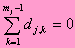 
.