The Three-Parameter Logistic model (3PL) uses an item response theory (IRT) model that specifies the probability of a correct response to a dichotomously scored multiple choice item as a logistic distribution. The 3PL extends the 2PL by introducing a guessing parameter. Items vary in terms of their discrimination, difficulty, and probability of guessing a correct response.
The 3PL (Birnbaum, 1968) extends the formulation of the 2PL by incorporating a guessing parameter, denoted as c. This parameter is the lower asymptote of the logistic item characteristic curve (icc) and represents the probability of examinees with low ability correctly answering an item. The parameter is included in the model to account for item response data from low ability examinees, where guessing is a factor in test performance.
The fundamental equation of the 3PL model is the probability that a randomly selected examinee with proficiency q on scale k will correctly respond to item j, characterized in terms of its discrimination (a), difficulty (b), and probability of guessing (c):
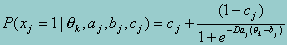
where
xj = the response to item j, 1 if correct and 0 if not;
aj = the slope of parameter of item j, characterizing its sensitivity to
proficiency, where aj>0;
bj = the threshold parameter of item j, characterizing its difficulty;
cj = the lower asymptote parameter of item j, reflecting the chances of
students with very low proficiency selecting the correct response;
D = an arbitrary scaling constant typically set to 1.7 to approximate results
from the normal ogive model.
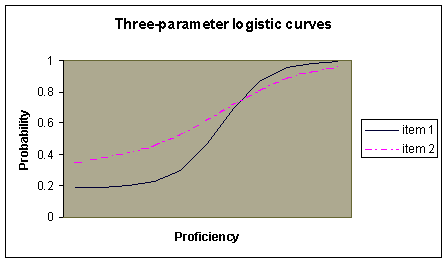
The figure below illustrates the 3PL logistic curve for two multiple choice items. The introduction of the c parameter adjusts the lower asymptote of the item characteristic curves to reflect the probability that a student with very low proficiency will select the correct response by chance alone. The higher the value of the lower asymptote in regards to the probability scale, the greater the chance of a low-proficiency student selecting the correct response. In this illustration, students with low proficiency have a greater chance of responding correctly to item 2 than to item 1.
Birnbaum, A. (1968). Some latent trait models and their use in inferring an examinee’s ability. In F. M. Lord & M. R. Novick, Statistical Theories of Mental Test Scores (pp. 397 - 472). Reading, MA: Addison-Wesley Publishing.
Crocker, L., & Algina, J. (1986). Introduction to Classical & Modern Test Theory. Fort Worth: Harcourt Brace Jovanovich College Publishers.
Hambleton, R. K., & Swaminathan, H. (1995). Item Response Theory: Principles and Applications. Norwell, MA: Kluwer Academic Publishers.
Currently the parameters of the Three-Parameter Logistic Model must be estimated through some other statistical software package and imported into AM. Future versions of AM software will allow the user to estimate both item and ability parameters.
NAEP uses the Three-Parameter Logistic model (3PL) to analyze multiple choice items scored correct or incorrect and that appear to allow for guessing. Since the item parameters and ability parameters are unobservable, there is a certain degree of indeterminacy in the model. This identification problem is solved in NAEP through Bayesian estimation by specifying prior belief for the parameters in the model. The prior distribution for the slope parameter, a, is specified as log normal with mean = 0 and standard deviation = 0.5. The prior for the threshold parameter, b, is specified as normal with mean = 0 and standard deviation = 2. The prior distribution for the lower asymptote, c, is specified as a beta distribution such that the mean of each item prior is the inverse of the number of alternatives, and the prior has the weight of 50 (by default) perfect observations of the responses for subjects of very low ability.