Item response theory is comprised of a set of statistical models that describe the relationship between assessment items and proficiency in some subject or skill area. In these models, proficiency is taken as a latent trait, indirectly observed through examinees performance on test items.
IRT models assume that an examinee’s performance on each item reflects characteristics of the item and characteristics of the examinee. While an infinite variety of models is possible, those in most common use, such as the one, two, and three-parameter logistic models, characterize items by the level of proficiency that they require and precision with which item performance reflects proficiency along that trait. Examinees are characterized by their proficiency. Examinee’s performance on a particular item reflects item difficulty, his or her proficiency, and the effects of other forces that are not correlated across items or individuals.
Item response theory (IRT) models, a class of latent trait models, were developed to estimate examinees’ proficiency based on item characteristics. Originally measured by the normal ogive function (Lord, 1952), item response models are more often measured by the logistic function (Birnbaum, 1968) due to its ease in computation. All models assume that all items on a subscale measure a common ability or proficiency and that the probability of a correct response on an item is uncorrelated with the probability of a correct response on another item, an assumption known as conditional independence. Items are measured in terms of their difficulty as well as their ability to discriminate among examinees of varying ability, and the probability that examinees with low ability will obtain a correct response through guessing. These three-parameters are typically denoted a for discrimination, b for difficulty, and c for guessing.
Traditional item response models can be understood as a technical adaptation of classical measurement theory to assessments comprised of a series of binary or ordinal measures. A simple decomposition of an observed score into a true score and an error component forms the heart of classical measurement theory (Spearman, 1904; Torgerson, 1958; Lord and Novik, 1968). More general classical measurement theory applies the same decomposition to any continuous measure. Thus, we can write:
yij = qi+eij(1)
where yij represents the value of a continuous, observed variable j for person i, q represents person i’s true score on the target trait, and eij is the corresponding measurement error. Suppose now that we have a binary measure, zij, in place of yij, observing instead
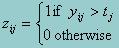
where tj is some threshold. Under this formulation, equation 1 becomes probabilistic:
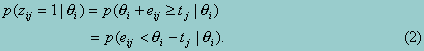
Equation 2 provides a general statement of the relationship between an individual’s response to an item and the target trait in traditional item response theory. Borrowing again from classical theory, IRT assumes the independence of eij across individuals and across items (the latter representing the assumption of local or conditional independence). The measurement error is also assumed to have a mean of zero, and is therefore assumed not to be a source of bias. By assuming conditional independence, the probability of a particular pattern of responses on a test, given q, is simply the product of individual probabilities across items.
The relationship between Equation 2 and IRT models becomes clear when we specify a probability distribution for eij. For example, if the distribution is specified as a logistic approximation to the normal distribution we see that:
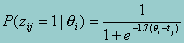
which is the formula for the Rasch (one-parameter) IRT model (Rasch, 1960), where the threshold (tj) corresponds to an item’s difficulty parameter.
Allen, M. J., & Yen, W. M. (1979). Introduction to Measurement Theory. Belmont, CA: Wadsworth, Inc..
Birnbaum, A. (1968). Some latent trait models and their use in inferring an examinee’s ability. In F. M. Lord & M. R. Novick (Eds.), Statistical Theories of Mental Test Scores (pp. 374 - 472). Reading, MA: Addison-Wesley Publishing.
Lord, F. M. (1952). A theory of test scores. Psychometric Monograph, No. 7.
Lord, F. M., & Novick, M. R. (1968). Statistical Theories of Mental Test Scores. Reading, Mass: Addison-Wesley.
Rasch, G. (1960). Probabilistic Models for Some Intelligence and Attainment Tests. Copenhagen: Denmarks Paedagogiske Institut.
Spearman, C. (1904). "General intelligence" objectively determined and measured. American Journal of Psychology, 15, 72-101.
Torgerson, W. S. (1958). Theory and Methods of Scaling. New York: Wiley.
Currently the parameters of the IRT Models must be estimated through some other statistical software package and imported into AM. Future versions of AM software will allow the user to estimate both item and ability parameters.